The Golden Ratio

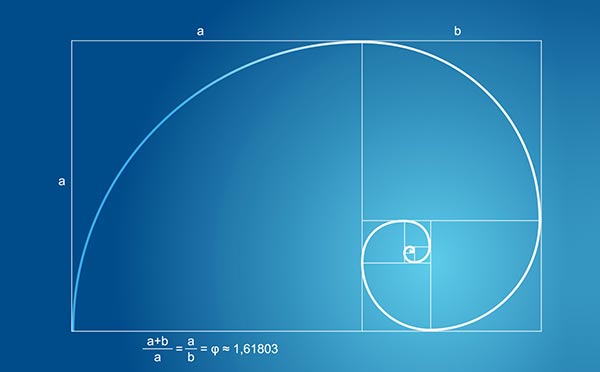You've probably heard that for thousands of years, mankind has been fascinated by the golden ratio, which is the value of 1 to φ (phi, pronounced 'fee' in the United States and its native Greek, and 'fye' in many other countries). φ is about 1.618. It's an irrational number that goes on forever, and is defined as:

A golden rectangle, whose sides are proportional to the golden ratio, is just a bit more squat than your high-definition TV screen. This rectangle is said to be the most aesthetically pleasing, and moreover, to be found throughout nature defining the proportions of all sorts of living creatures including the ideal human face. Great composers, artists, and architects are said to have based their work upon this ratio. Players of financial markets create formulas that rely upon it. Throughout your home, you'll find many objects whose shape is tantalizing similar to a golden rectangle: books, appliances, electric outlet covers, playing cards, paintings, windows. People have found it in the structure of DNA and the arrangement of molecules in crystals. Most famously of all, the Greek Parthenon, the preeminent icon of architecture, is said by some to be based almost entirely on the golden ratio. This ratio is believed by many to be so ubiquitous in both nature and design that it's also been called the divine proportion.

φ and the golden ratio are best known by their unique mathematical and geometrical properties. If you take a rectangle whose sides are proportional to the golden ratio, you can cut a square off one end of it, and the resulting small rectangle that remains is of the exact same proportions as the original. You can cut a square off of that and you'll get a still smaller golden ratio rectangle, and you can do this ad infinitum. That's its basic geometric property.

The essential mathematical property of φ is that it is the ratio of successive numbers in the Fibonacci series. The Fibonacci series consists of values equal to the sum of the two preceding values: 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. 5+8=13, 8+13=21, 13+21=34, and on and on. As this series continues infinitely, the ratio of each number to the previous one gets closer and closer to φ; but as the series is infinite, it never quite gets there. So φ is the limit of the ratio of that sequence. By the 40th value in the Fibonacci series, which is 102,334,155, φ is accurate to 15 decimal places.

Here is perhaps the most interesting manifestation of phi in nature. It has to do with efficient packing. When you look straight down at a tree from above, the tree is most efficient if as many leaves as possible are visible and not shaded by other leaves. As a stem grows, it follows a genetic formula to know how often to produce a leaf and at what angle from the preceding leaf. If it produced each leaf at intervals such as 1/4 turn, every leaf would end up shaded by the fourth leaf above it. In fact, no matter what integer fraction of a full turn we use, we end up eventually repeating a pattern and shading leaves. So evolution eventually resulted in a more efficient genetic instruction: φ. Produce φ leaves per turn — just over 137.5° between successive leaves — and no two leaves will ever shade each other. This angle is called the golden angle.

We see a very specific and obvious example of this pattern in the seeds in the center of a sunflower. Florets, which mature into seeds, grow from the center of the sunflower, and each new one pushes the existing seeds outward. The result of each new seed growing a golden angle away from its predecessor is a sunflower with seeds packed as efficiently as possible within the circular head of the flower, no matter how the large the flower gets. This type of packing produces visibly criss-crossing spiral patterns going both directions around the head. Not coincidentally, at any size of flower, the number of clockwise spiral arms and counter-clockwise spiral arms are always two consecutive Fibonacci numbers. Seeds in a pine cone, and other similar structures from the plant world, follow the same blueprint.

This tendency for ratios based on φ to eliminate repetition has engineering applications. One of the most familiar is in the design of sound rooms for listening to music or watching movies, rooms in which we want to cancel out standing audio waves and resonances. Audio engineers refer to the golden room ratio, which establishes the basic ideal dimensions of a sound room to be 10 × 16 × 26. The height of the room 10 × φ ≈ 16, giving the length of the room, and 16 × φ ≈ 26 which gives the width of the room. Any diagonal straight-line path traveled inside a golden rectangle will reflect infinitely without ever repeating its course, and so sound waves inside a room of such dimensions are always dispersed as efficiently as possible.

Despite many books and articles claiming otherwise, the exact history of man's understanding of the golden ratio is not known. Around 500 BCE, the Greek mathematician Pythagoras established the Pythagorean school of thought, the symbol for which was a pentagram. When you inscribe a star inside a pentagon, the ratio of all the line segments is the golden ratio; so although it seems he must have known about the ratio, Pythagoras himself left no writings that tell us for certain. A more concrete early definition comes from Euclid who established the golden ratio in his book Elements around 300 BCE, calling it the extreme and mean ratio. It seems almost certain that they would have had to have known about the Fibonacci series; however it wasn't until around 1200 that Leonardo Fibonacci described the famous sequence that now bears his name, but none of Fibonacci's writings show that he ever made its connection with φ or the golden ratio. Today the concepts and relationships are well understood, and they are now common mathematical devices.

The appearance of the golden ratio in the natural world has led, almost inevitably, to its adoption and co-opting by many alternative researchers in just about every discipline. Perhaps the best known pseudoscientific claim about the golden ratio is that the Greek Parthenon, the famous columned temple atop the Acropolis in Athens, is designed around this ratio. Many are the amateurs who have superimposed golden rectangles all over images of the Parthenon, claiming to have found a match. But if you've ever studied such images, you've seen that it never quite fits, at least not any better than any other rectangle you might try. That's because there's no credible historical or documentary evidence that the Parthenon's designers, who worked more than a century before Euclid was even born, ever used the golden ratio in any way, or even knew of its existence.

Another pseudoscientific claim is that the golden ratio is found throughout the human body. Volumes of nonsense have been written claiming that all sorts of arbitrary body measurements betray the golden ratio. The width of the shoulders compared to the height of the head; the height of the navel relative to the height of the whole body; the length of the forearm compared to the distance from the head to the fingertips; and so on, and so on, and so on. Obviously these measurements are different on everyone; there is probably not a single living human for whom these many claims are true. Moreover, it's completely arbitrary. Give me any number, any ratio, or any shape, and I can just as easily come up with an equally long list of body features that's equally accurate.

The example of a book is another good one. The height and width of a common book is determined by convenience; we want it to be conveniently proportioned when closed (not too tall) and open (not too wide). Some cite 1:φ as the ideal book shape, but this is wrong. A book sized so that it's the same proportions whether open or closed is 1:√2, not 1:φ. φ is significantly larger than √2. In the paper industry, 1:√2 is called the Lichtenberg ratio.

The simple fact is that rectangles that are neither too square nor too narrow are the most attractive, and often the most usable in design. The golden ratio falls within the range of generally pleasing rectangles, but so does √2, √3, and a lot of other numbers. There is no need to claim that a single perfect ratio exists that is best for all applications.

A good way to tell real manifestations of the golden ratio from made-up or assumed ones is whether it serves a purpose that could not also be served by a similar number. The sunflower's employment of the golden angle is for a very specific purpose, and it absolutely requires the number φ. An example of a mistaken manifestation is the claim that each of your finger joints is longer than the next by the golden ratio. Not only is this measurably wrong, but it would provide no specific benefit for this to be the case, and thus no such thing evolved. The benefit of improved accuracy at increasingly small scales of manipulation means it's useful to have progressively smaller finger segments, so that's what we have. But there's no need for that to be the golden ratio, or even all exactly the same, so they're not.

Another pseudoscientific example from nature is that of the spiraling seashell. A golden spiral is one which becomes φ times wider with each quarter turn, and it's often said that the nautilus shell follows this. Not true. A golden spiral is only one of an infinite number of possible logarithmic spirals. It's beneficial for the nautilus to be able to maintain the same shape as it grows, and this purpose is served by any approximately logarithmic spiral. Having its spiral's growth factor be based on φ would confer no additional benefit.

φ, the golden ratio, and the Fibonacci series are mathematically interesting and do have natural manifestations. That doesn't mean everything, or even anything else, is based on them. The popularity and "big name" of the "divine proportion" has been the real driver of its pseudoscientific assignment to just about anything and everything. Those whose brains' pattern-matching software is in overdrive have probably heard of the golden ratio, and so it's the one they think of whenever they see a rectangle, or a great work of art (like the Mona Lisa, which is not based on the golden ratio), or patterns in the stock market (which don't exist at all, let alone at the golden ratio), or in the numerology of the Bible (unless any other number is allowed to be considered just as significant). Not every claim about the golden ratio is the result of hyperactive pattern matching, but most are. At a minimum, such a claim is always a good tipoff that you should be skeptical.

By Brian Dunning
Follow @BrianDunning